I. Giới thiệu:
Cây đỏ đen (RB Tree) là một dạng cây nhị phân tìm kiếm tự cân bằng, RB Tree được giới thiệu vào năm 1972 bởi Rudolf Bayer.
Các phép toán trên chúng như tìm kiếm (search), chèn (insert), và xóa (delete) trong thời gian O (log n), trong đó n là số các phần tử của cây.
II. Tổng quan về RB Tree:
1. Các tính chất:
RB Tree là một cây tìm kiếm nhị phân (BST) nên trước hết nó thừa hưởng hết mọi tính chất của một BST thông thường. Chúng ta sẽ nói về các tính chất riêng của RB Tree. Trước hết, mỗi nút của RB Tree có thêm một thuộc tính là color. Color nhận một trong hai giá trị là Red và Black. Ngoài ra:
Ngoài ra:
- Một nút hoặc là đỏ hoặc là đen.
- Gốc là đen.
- Tất cả các node NULL là đen.
- Không tồn tại một đường đi trên cây đi từ gốc đến nút NULL mà có 2 nút liên tiếp là màu đỏ (và suy ra mọi nút đỏ đều có nút cha là đen, không có con hoặc có 2 nút con là đen).
- Xét một nút bất kì, ta luôn có tất cả các đường đi từ nút đó đến các nút NULL sẽ có số lượng nút màu đen bằng nhau (ở đây và cả trong bài viết này, đường đi có nghĩa là đi xuống node sâu hơn)
2. Sự cân bằng của RB-Tree.
Trước hết, cần lưu ý rằng, sự cân bằng của RB Tree không phải là tuyệt đối như cây AVL. Từ 5 tính chất trên, ta có thể rút ra được các nhận xét như sau:
-
Gọi A là độ dài đường đi dài nhất từ gốc đến một nút NULL, B là độ dài đường đi ngắn nhất từ gốc đến một nút NULL. Ta sẽ có A <= 2B. Chứng minh: Dựa vào tính chất 4 và 5, ta thấy rằng một đường đi dài nhất có thể sẽ có các nút đỏ, đen xen kẽ nhau mà gốc là nút đen, nên số nút đỏ trên một đường đi tối đa bằng số nút đen trên đường đi đó (không thể có hai nút đỏ liên tiếp). Và đường đi ngắn nhất có thể sẽ chỉ gồm các nút đen. Mà số nút đen của hai đường đi này là bằng nhau, nên đường đi dài nhất có thể sẽ hơn đường đi ngắn nhất một lượng bằng số nút đỏ trên đường đi đó (số nút đỏ này không vượt quá số nút đen) nên từ đó ta suy ra được tính chất trên (maxA <= 2minB -> A <= 2B đây là một logic thông thường).
-
Một nút nếu có duy nhất 1 con thì nút con đó phải là nút lá có màu đỏ. Xét một nút S, gọi 2 nút con của S là SL và SR. Không mất tính tổng quát, giả sử nút con khác NULL của S là SL và SR là nút NULL. Khi đó nếu SL có màu đen thì đường đi từ gốc đến một nút NULL mà đi qua SL sẽ nhiều hơn ít nhất là 1 nút đen so với đường đi đến nút NULL SR. Còn nếu SL không phải là lá, thì SL sẽ có ít nhất một nút con C. Khi đó giữa SL và C phải có ít nhất một nút đen và cũng dễ dàng chứng minh được đường đi đến nút NULL qua C sẽ đi qua nhiều nút đen hơn đường đi đến SR.
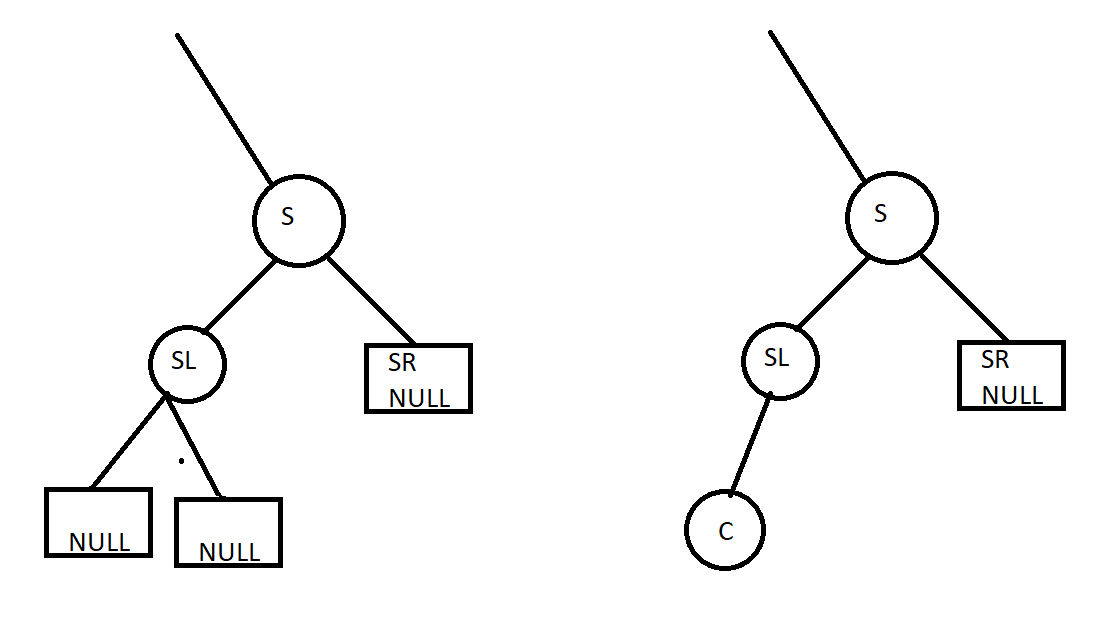
Cũng từ tính chất 2 ta có thể nhận thấy rằng, nếu gọi độ dài đường đi ngắn nhất từ gốc đến một nút lá nào đó là H thì tất cả các đỉnh có khoảng cách tới gốc không vượt quá $H$ sẽ tạo thành cây nhị phân đầy đủ có độ cao H. Kết hợp với nhận xét đầu tiên thì RB Tree sẽ có độ cao trong khoảng [log(n+1), 2log(n+1)] - nói cách khác, độ cao của RB Tree sẽ không thể vượt quá 2log(n+1).
Tham khảo thêm: https://doctrina.org/maximum-height-of-red-black-tree.html
III. Thao tác trên RB Tree:
1. Biểu diễn RB Tree:
Kiểu dữ liệu của các nút trên cây:
class Node {
private:
int color;
int data;
Node *leftChild;
Node *rightChild;
Node *parent;
public:
Node(int color, int data) {
this->color = color;
this->data = data;
this->leftChild = NULL;
this->rightChild = NULL;
this->parent = NULL;
}
friend class RBTree;
};
Dữ liệu của lớp biểu diễn cây chỉ cần lưu lại nút gốc:
class RBTree {
private:
Node *root;
};
2. Phép quay cây
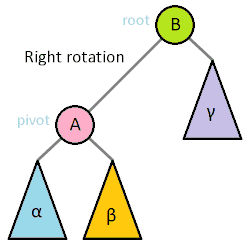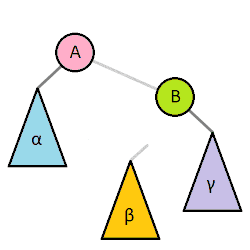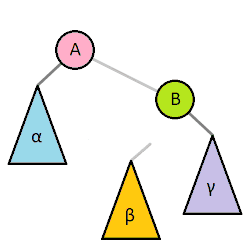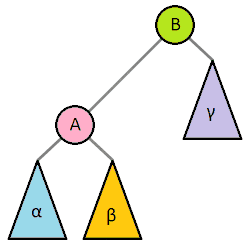
Các bạn có thể xem thêm phần này tại đây. Mục đích của phép quay cây là để chỉnh sửa cây BST lại (mục đích thường là hướng tới việc giảm độ cao) mà cây mới sau khi quay vẫn là cây BST. Quay cây gồm có quay qua trái và quay qua phải. Phép quay sẽ được diễn ra như sau:
2.1 Quay trái
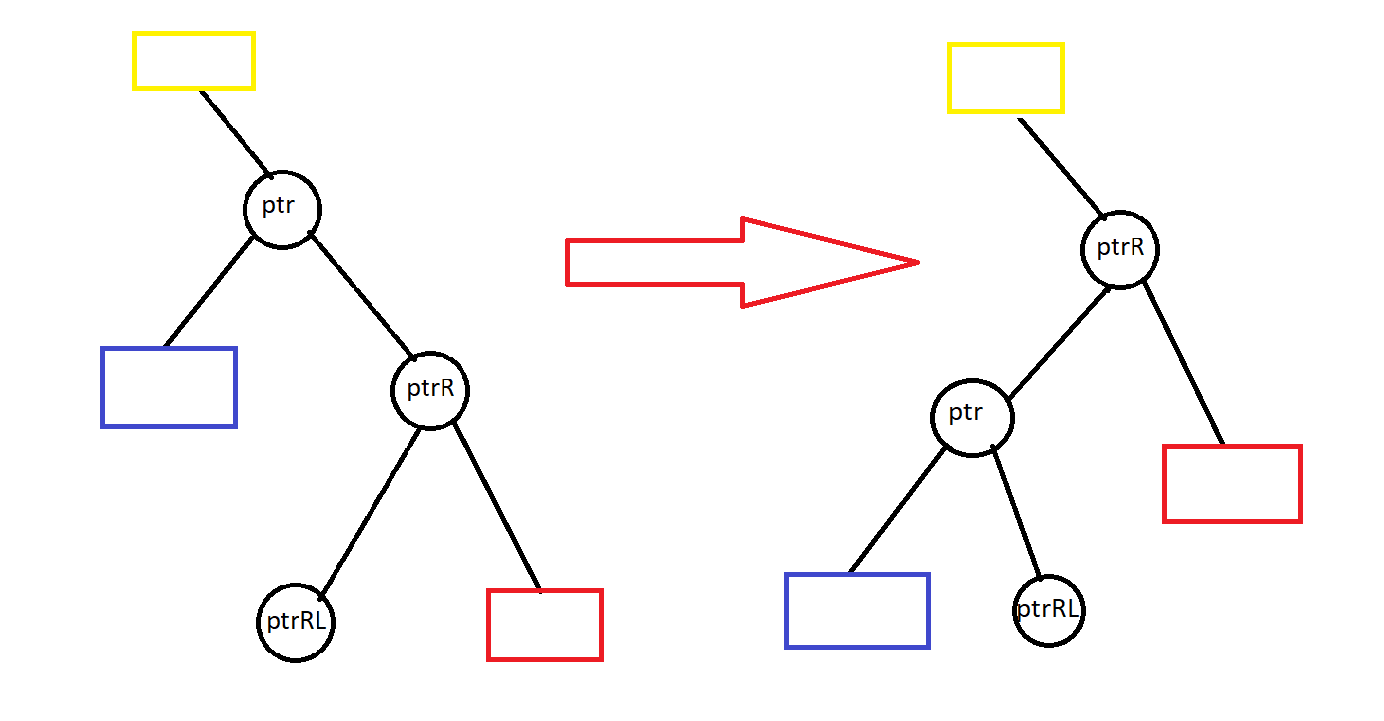
- Quay trái cây tại nút ptr:
- Đặt con phải của ptr thành ptrRL.
- Nếu ptrRL không phải NULL thì đặt cha của ptrRL là ptr.
- Nếu ptr là gốc thì đặt lại gốc mới là ptrR. Ngược lại, tùy theo ptr là con trái hay con phải của cha nó mà đặt lại con trái/phải đó thành ptrR.
- Đặt lại con trái của ptrR thành ptr, cha của ptrR thành cha cũ của ptr, cha mới của ptr thành ptrR.
void RBTree::rotateLeft(Node *&ptr) {
Node *rightChild = ptr->rightChild;
ptr->rightChild = rightChild->leftChild;
if (ptr->rightChild != NULL)
ptr->rightChild->parent = ptr;
if (ptr == this->root)
this->root = rightChild;
else if (ptr == ptr->parent->leftChild)
ptr->parent->leftChild = rightChild;
else
ptr->parent->rightChild = rightChild;
rightChild->leftChild = ptr;
rightChild->parent = ptr->parent;
ptr->parent = rightChild;
}
2.2 Quay phải
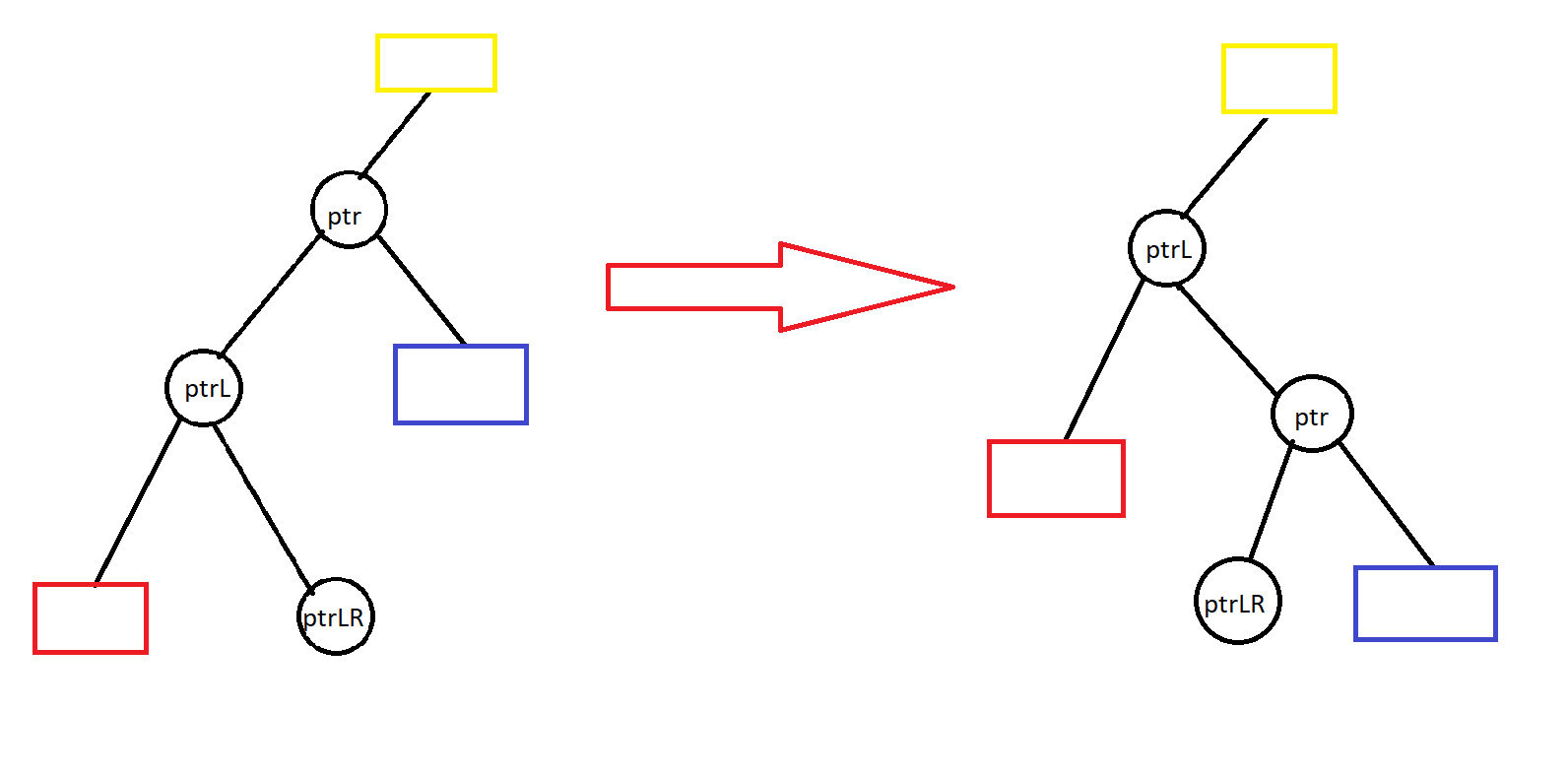
- Quay phải cây tại nút ptr:
- Đặt con trái của ptr thành ptrLR.
- Nếu ptrLR không phải NULL thì đặt cha của ptrLR là ptr.
- Nếu ptr là gốc thì đặt lại gốc mới là ptrL. Ngược lại, tùy theo ptr là con trái hay con phải của cha nó mà đặt lại con trái/phải đó thành ptrL.
- Đặt lại con phải của ptrL thành ptr, cha của ptrL thành cha cũ của ptr, cha mới của ptr thành ptrL.
void RBTree::rotateRight(Node *&ptr) {
Node *leftChild = ptr->leftChild;
ptr->leftChild = leftChild->rightChild;
if (ptr->leftChild != NULL)
ptr->leftChild->parent = ptr;
if (ptr == this->root)
this->root = leftChild;
else if (ptr == ptr->parent->leftChild)
ptr->parent->leftChild = leftChild;
else
ptr->parent->rightChild = leftChild;
leftChild->rightChild = ptr;
leftChild->parent = ptr->parent;
ptr->parent = leftChild;
}
3. Insert
3.1 Chọn vị trí.
Khi thêm một giá trị vào RB Tree, ta cần chú ý cây có rỗng hay không, nếu cây đang rỗng thì ta chỉ cần cho nút đó trở thành gốc và gán cho nó màu đen.
Trong trường hợp cây không rỗng, ta sẽ duyệt như duyệt cây BST để tìm vị trí thích hợp trên cây. Cụ thể, gọi x là giá trị cần thêm vào cây. Bắt đầu từ linker = root, nếu x < linker->data thì ta đi về phía bên trái của linker. Trong trường hợp linker->leftChild là một nút NULL thì ta cho luôn nút mới vào vị trí này. Còn nếu x >= linker->data thì ta cho linker đi về nhánh phải, nếu nhánh này NULL thì cho luôn nút mới vào vị trí này.
Sau khi đã thêm được nút vào cây, ta cần chỉnh lại cấu trúc của cây để cây thỏa 5 tính chất ở trên bằng cách quay cây và đổi màu của nút. Cụ thể hơn sẽ được nói ở phần tiếp theo.
Lưu ý, mặc định thì nút mới sẽ có màu là đỏ.
void RBTree::insert(int data) {
Node *ptr = new Node(RED,data);
if (root == NULL) {
root = ptr;
root->color = BLACK;
return;
}
Node *linker = root;
while (linker != NULL) {
if (data < linker->data) { // go left
if (linker -> leftChild == NULL) {
linker->leftChild = ptr;
break;
} else
linker = linker->leftChild;
} else { // go right
if (linker->rightChild == NULL) {
linker->rightChild = ptr;
break;
} else
linker = linker->rightChild;
}
}
ptr->parent = linker;
insertFix(ptr);
}
3.2 Chỉnh cây:
Trước hết ta có cách gọi các nút liên quan đến một nút X nào đó như sau:
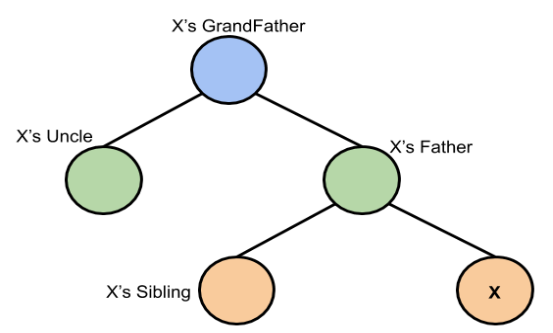
3.2.1 Nút cha có màu đen:
Khi nút cha của nút X vừa được thêm vào có màu đen thì cây vẫn thỏa mãn đủ 5 tính chất, nên ta không cần làm gì thêm ở bước này nữa.
3.2.2 Nút cha có màu đỏ:
3.2.2.1 Nút uncle có màu đỏ:
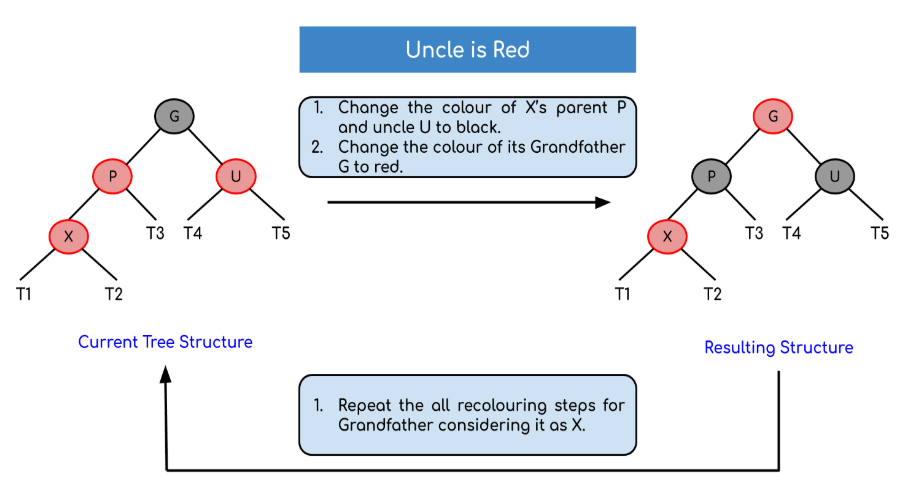
Trường hợp này ta sẽ đổi màu các nút P, U, G sau đó coi G như là X mới và xử lí tiếp trên nút X mới này.
3.2.2.1 Nút uncle có màu đen:
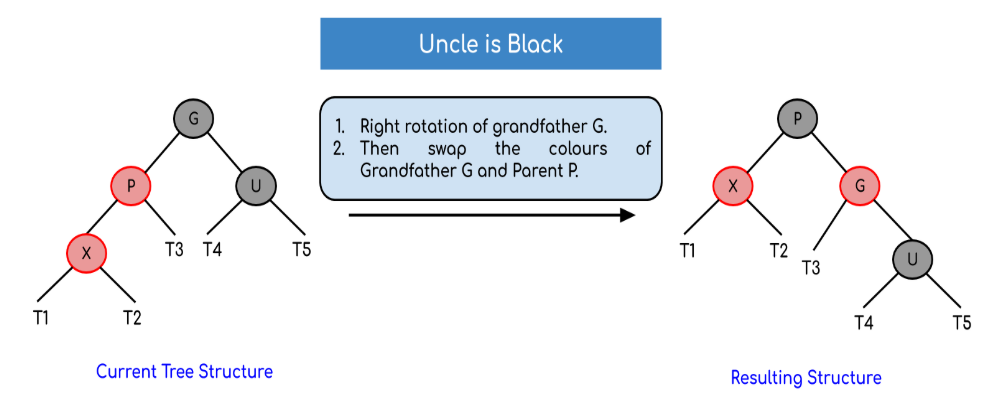
Cần lưu ý rằng, trường hợp này không xảy ra ngay từ đầu mà nó sẽ xảy ra sau khi gặp trường hợp 3.2.2.1 một số lần. Tức là sau khi ta thực hiện đổi màu trong trường hợp trên thì mới có khả năng xuất hiện trường hợp này (các bạn có thể tưởng tượng thật ra trước đó nút X là màu đen chữ không phải màu đỏ như hình vì thật chất nó là nút G cũ trong trường hợp trên mà sau đó nó mới được gán thành nút X). Và hiện tại thì đường đi từ X đến NULL vẫn có số đỉnh đen bằng với đi từ U xuống NULL.
Ta sẽ có 4 trường hợp như sau:
- P là con trái của G, X là con trái của P:
- Đổi màu G và P.
- Quay phải G.
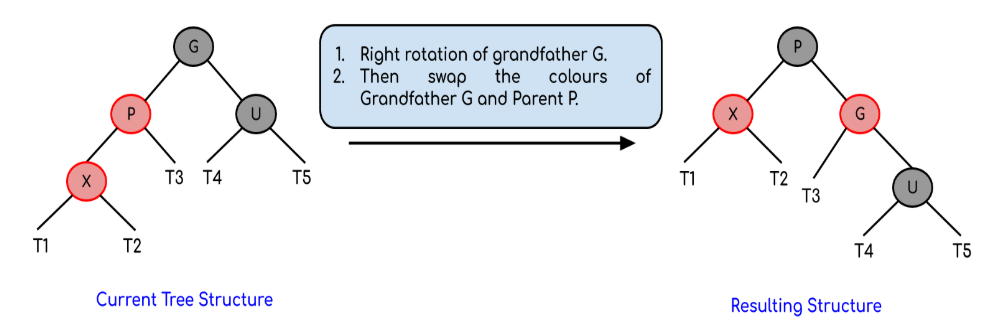
- P là con trái ủa G, X là con phải của P:
- Quay trái P.
- Swap (đổi tên lại) P và X (X mới là P cũ và ngược lại).
- Lúc này xử lí tiếp như trường hợp 1.
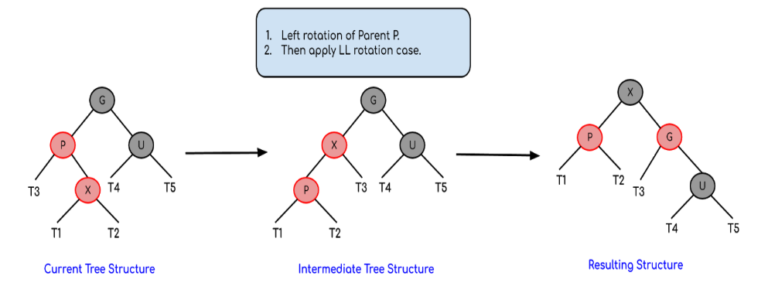
- P là con phải của G, X là con phải của P:
- Đổi màu G và P.
- Quay trái G.
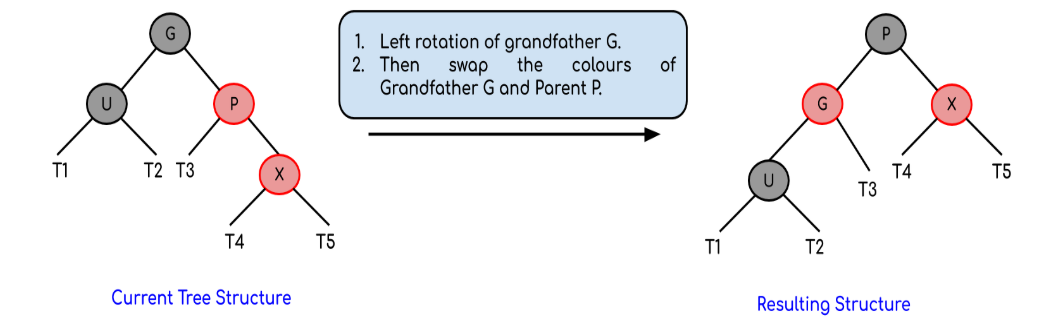
- P là con phải ủa G, X là con trái của P:
- Quay phải P.
- Swap (đổi tên lại) P và X (X mới là P cũ và ngược lại).
- Lúc này xử lí tiếp như trường hợp 3.
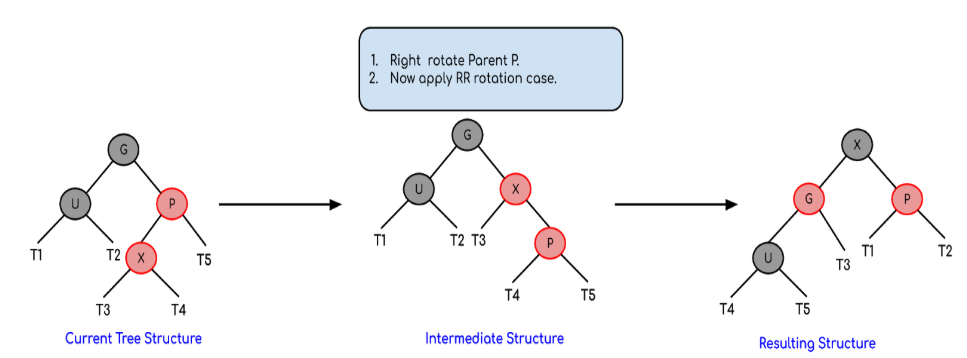
3.3 Giải thích thêm:
- Hình trong trường hợp 2 bị sai vị trí các nút T1, T2, T3 sau khi quay cây, nhưng không cần quan tâm đến các nút đó.
3.4 Code:
void RBTree::insertFix(Node *&ptr) {
while (ptr != root && getColor(ptr) == RED && getColor(ptr->parent) == RED) {
Node *parent = ptr->parent;
Node *grandparent = parent->parent;
if (parent == grandparent->leftChild) {
Node *uncle = grandparent->rightChild;
if (getColor(uncle) == RED) {
setColor(uncle, BLACK);
setColor(parent, BLACK);
setColor(grandparent, RED);
ptr = grandparent;
} else {
if (ptr == parent->rightChild) {
rotateLeft(parent);
ptr = parent;
parent = ptr->parent;
}
rotateRight(grandparent);
setColor(grandparent, RED);
setColor(parent, BLACK);
ptr = parent;
}
} else {
Node *uncle = grandparent->leftChild;
if (getColor(uncle) == RED) {
setColor(uncle, BLACK);
setColor(parent, BLACK);
setColor(grandparent, RED);
ptr = grandparent;
} else {
if (ptr == parent->leftChild) {
rotateRight(parent);
ptr = parent;
parent = ptr->parent;
}
rotateLeft(grandparent);
setColor(grandparent, RED);
setColor(parent, BLACK);
ptr = parent;
}
}
}
setColor(root, BLACK);
}
4. Delete
4.1 Tiền xử lí
Khi xóa một nút V bất kì, nếu nút V đó có cả 2 nút con thì ta hoàn toàn có thể đi tới nút X là nút có giá trị nhỏ nhất trong cây con của nút con phải hoặc nút X là nút có giá trị lớn nhất trong cây con của nút con trái. Gán V->data = X->data. Sau đó xóa nút X đi. Như vậy cũng tương đương với việc xóa trực tiếp nút V.
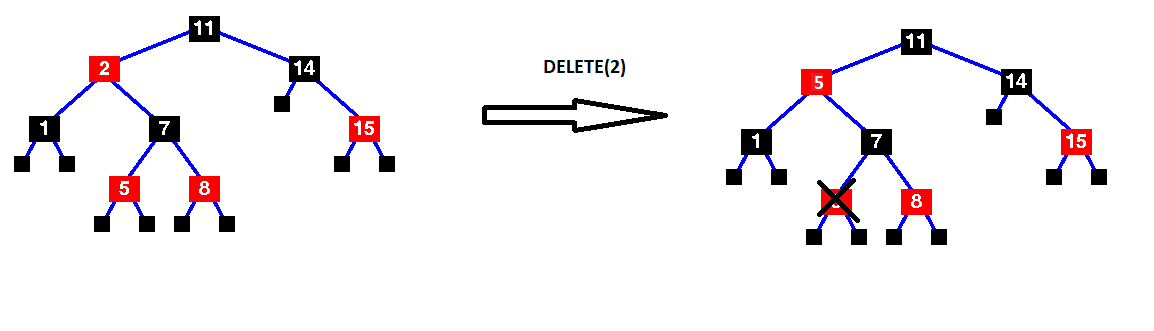
Chú ý: Nếu nút V chỉ có 1 con thì ta cũng có thể làm tương tự như vậy nhưng chỉ có 1 lựa chọn (nhỏ nhất nhánh phải hoặc lớn nhất nhánh trái). Nhưng điều này cũng không cần thiết lắm vì nếu có 1 nút con duy nhất thì nút đó phải là nút lá màu đỏ, và nó sẽ thuộc trường hợp đơn giản sẽ được nói sau đây, nên việc tìm nút để thay thế là không cần thiết.
Vậy giờ ta chỉ cần quan tâm đến việc xóa nút có nhiều nhất 1 nhánh con.
Gọi U là nút con duy nhất của nút V cần xóa (nếu V không có nút con nào thì U là nút NULL và sẽ có màu đen).
Như vậy việc đầu tiên cần làm sau khi xóa V đó là để U thay vào vị trí của V sau đó ta sẽ tiến hành chỉnh cây lại nếu cần.
Nếu V và U có một nút mang màu đỏ (cả hai nút không thể cùng có màu đỏ được). Ta sẽ đổi màu của U thành đen khi đó các ràng buộc sẽ được đảm bảo. Như đã nói ở phần chú ý, nếu có duy nhất một con thì con đó phải là nút lá màu đỏ nên trường hợp này đã giải quyết được 2 trường hợp: V là lá màu đỏ, V có một nút con.
Vậy thì chỉ còn lại trường hợp V đen và không có con nào cả (U là NULL). Khi đó ta sẽ gọi hàm eraseFix
void RBTree::eraseNode(Node *&ptr) {
Node* child = (ptr->leftChild == NULL) ? ptr->rightChild : ptr->leftChild;
Node* parent = ptr->parent;
// case one of ptr & child red
if (ptr->color == RED || getColor(child) == RED) {
//child->parent = parent;
setParent(child, parent);
// case ptr is root
if (parent != NULL)
if (parent->leftChild == ptr)
parent->leftChild = child;
else
parent->rightChild = child;
else
root = child;
setColor(child, BLACK); // child is red then set child as black
delete ptr; // delete because we return right now
return;
}
// luc nay ptr va child deu la mau den, nen se goi ham eraseFix
Node *sibling = getSibling(ptr); // de tien hon cho ham eraseFix
if (parent != NULL)
if (parent->leftChild == ptr)
parent->leftChild = NULL;
else
parent->rightChild = NULL;
else
root = child;
delete ptr;
eraseFix(parent, sibling);
}
void RBTree::erase(int data) {
Node *ptr = find(data);
if (ptr->leftChild != NULL && ptr->rightChild != NULL) {
Node *beErase = minimumRight(ptr);
ptr->data = beErase->data;
ptr = beErase;
}
eraseNode(ptr);
}
4.2 Chỉnh cây
Nhắc lại một lần nữa, khi đã gọi hàm eraseFix thì chắc chắn rơi vào trường hợp cả V và U đều là màu đen (V là lá và U là NULL), nhánh của U ít hơn nhánh của sibling một nút đen. Gọi sibling của U là S, cha của sibling là P, con trái và con phải của S lần lượt là SL và SR (2 nút con này có thể là NULL hoặc RED)
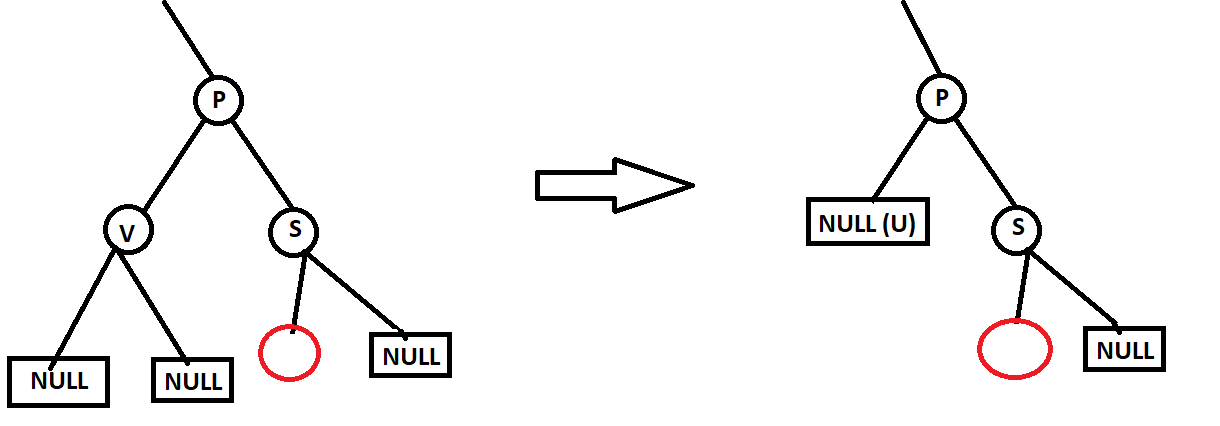
4.3.1 SL và SR có ít nhất một nút màu đỏ
-
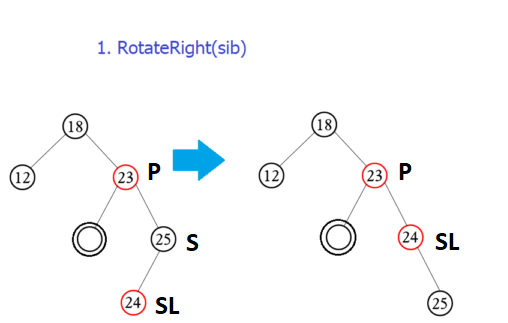
S là con trái của P, SL có màu đỏ:
- S->color = P->color
- P->color = BLACK (P đang đen thì vẫn là đen, đang đỏ thì cũng sẽ thành đen)
- SL->color = BLACK
- Quay phải P.
-
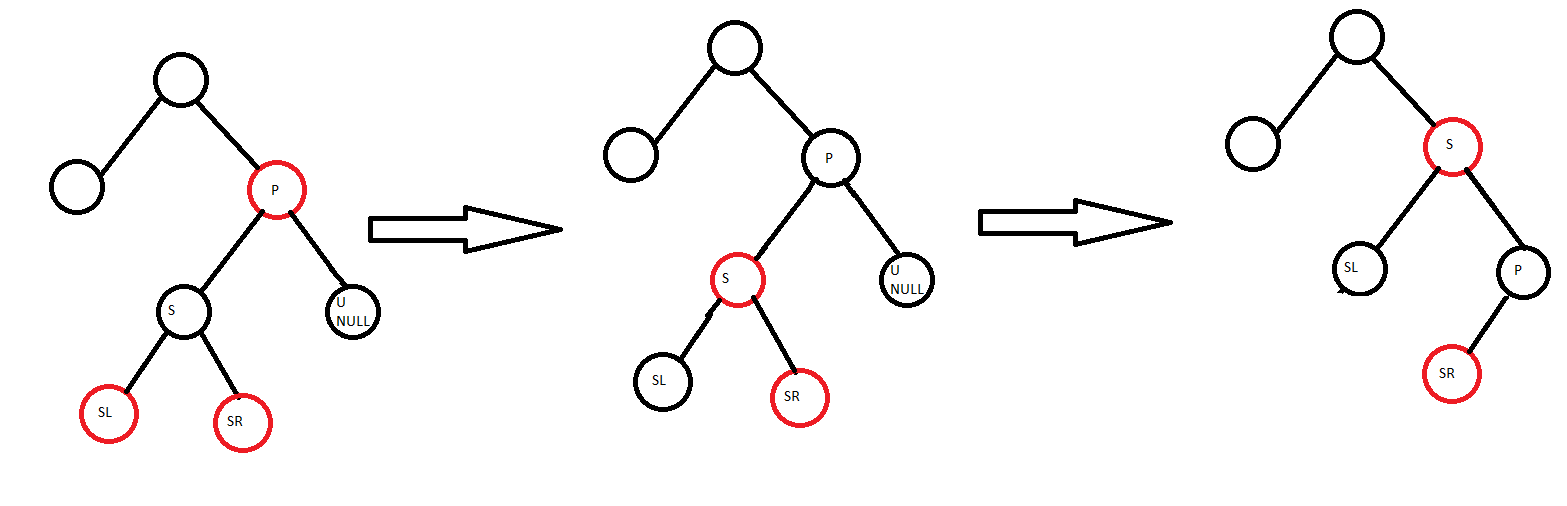
S là con trái của P, chỉ có SR màu đỏ:
- Quay trái S sẽ được như cây thứ 2 ở hình bên dưới.
- Đặt lại S = SR và cập nhập lại SL, SR theo S mới.
- Đưa về trường hợp phía trên, làm như trên với S, SL mới và P.
-
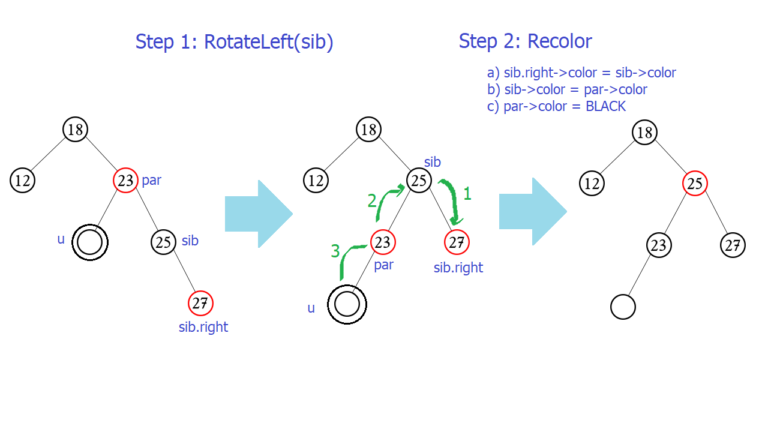
S là con phải của P, SR có màu đỏ:
- S->color = P->color
- P->color = BLACK
- SR->color = BLACK (trong hình nó là bằng sib->color, nhưng mà SR đã đỏ rồi thì S phải đen)
- Quay trái P
-
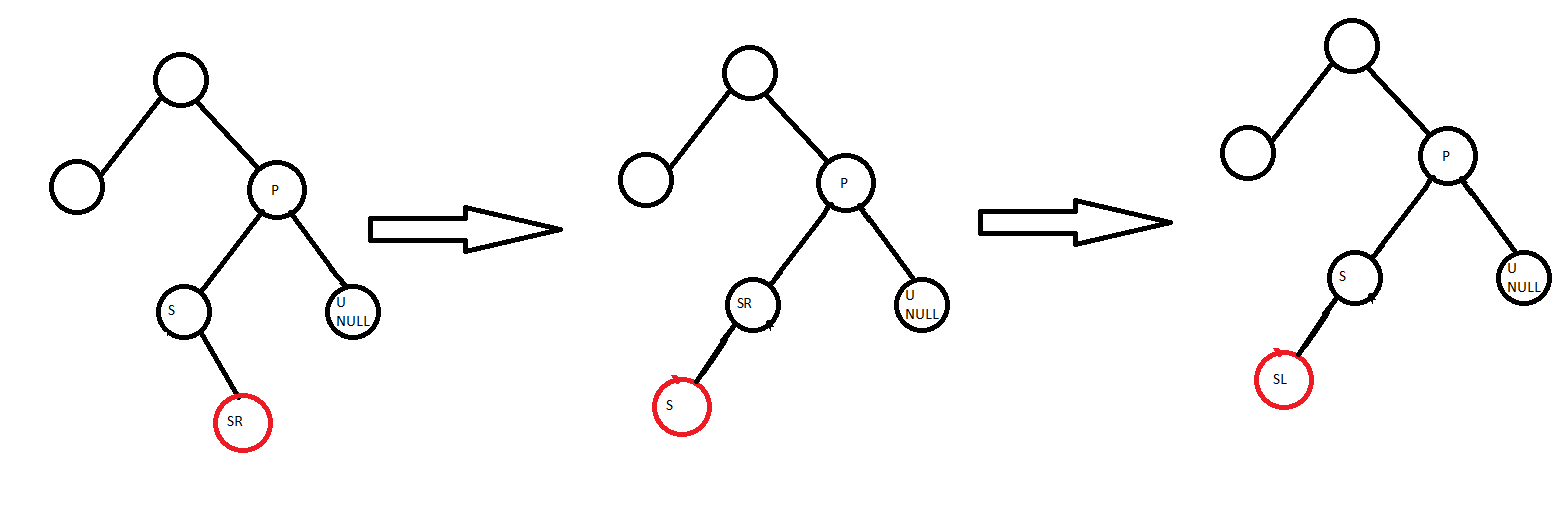
S là con phải của P, chỉ có SL màu đỏ:
- Quay phải S sẽ được như cây thứ 2 ở hình bên dưới.
- Đặt lại S = SL và cập nhập lại SL, SR theo S mới.
- Đưa về trường hợp phía trên, làm như trên với S, SR mới và P.
P/S: Đổi màu trước hay quay trước đều được cả, không ảnh hưởng đến kết quả. Trong trường hợp 1 và 3, nếu cả hai nút con của S đều là đỏ thì cũng không ảnh hưởng đến kết quả, nhưng nếu nút con ở vị trí thuận không phải màu đỏ (trường hợp 2 và 4) thì phải xoay cây để đưa về trường hợp thuận chiều (1 và 3).
4.3.2 S, SL và SR đều có màu đen:
Thì SL và SR đều là NULL, ta sẽ xử lí trường hợp này như sau:
- S->color = RED
- Nếu P là màu đỏ thì đổi màu P: P->color = BLACK
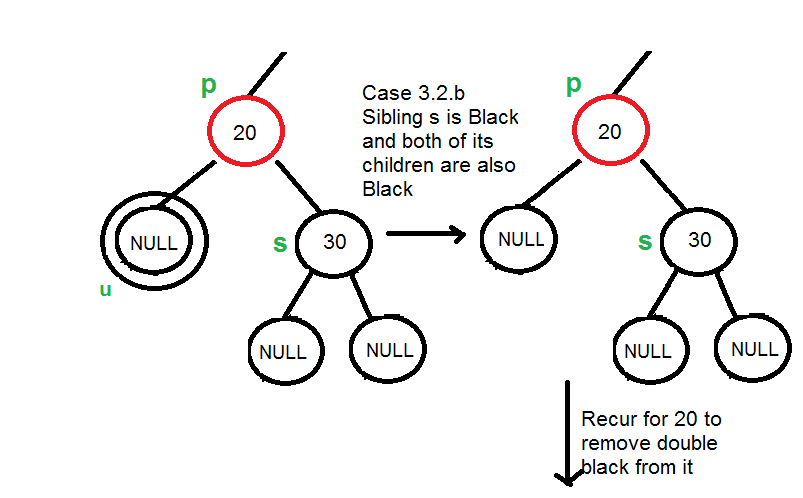
- Nếu không thì gọi hàm eraseFix với P mới là P->parent và S mới là sibling của P.
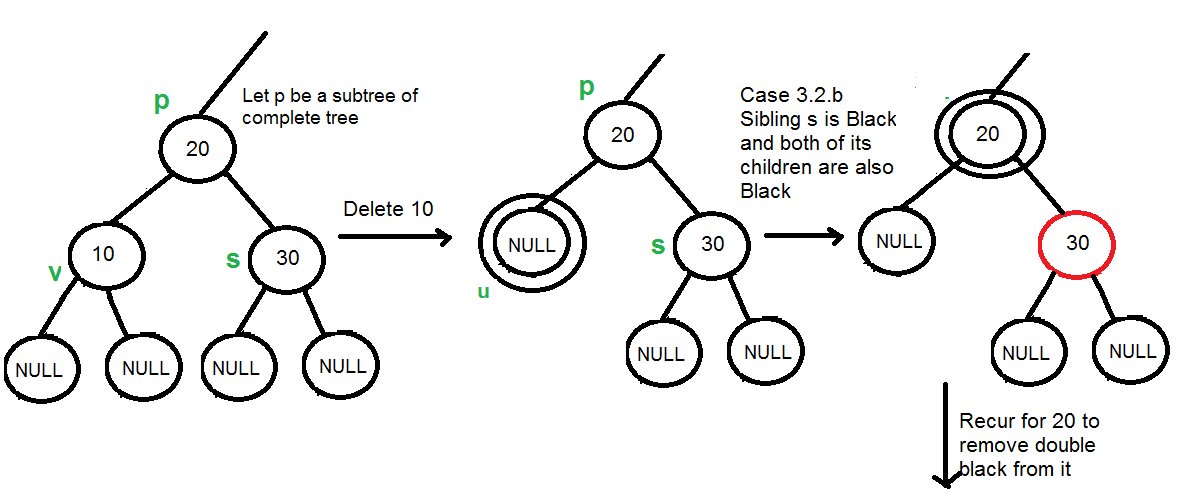
Trước hết cần lưu ý rằng, đường đi đến nút NULL có qua S là một đường đi chuẩn, tức là nó có số nút đen bằng với các đường đi từ root đến các nút NULL khác.
Vậy thì ta chỉ cần fix làm sao mà từ P đến S không thay đổi số lượng nút đen và từ P đến U tăng thêm 1 nút đen vì từ P đến U đang ít hơn 1 nút đen so với từ P đến S.
Còn nếu không có khả năng làm việc đó, thì ta giảm số nút đen đến S đi 1 rồi tăng số nút đen đến P lên 1 mà không ảnh hưởng đến số nút đen đến U khi đó chỉ tính riêng cây con gốc P thì đã bằng, nên nếu P đang là gốc rồi thì không cần phải chỉnh nữa.
4.3.3 S có màu đỏ:
Trường hợp này thì đơn giản thôi (vì nó là cái cuối rồi)
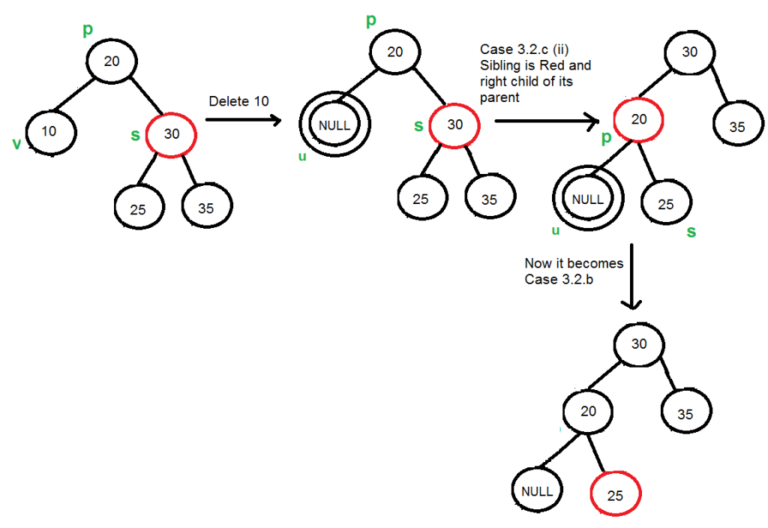
S là màu đỏ thì P, SL, SR đều là màu đen, xử lí như trên là được:
-
Nếu S là con phải của P:
- Quay trái P.
- P->color = RED
- S->color = BLACK
- Đưa về trường hợp S đen như 4.3.2 (cái hình thứ 3 ấy, không phải hình thứ 4 đâu) với S mới là SL cũ (cái hình là nó tự chỉnh SL thành S luôn rồi)
-
Nếu S là con trái của P:
- Quay phải P.
- P->color = RED
- S->color = BLACK
- Đưa về trường hợp S đen như 4.3.2
void RBTree::eraseFix(Node *&parent, Node *sibling) {
if (parent == NULL) return;
//cout << parent->data << " " << sibling->data << " " << "\n";
//Node *sibling = (parent->leftChild == NULL) ? parent->rightChild : parent->leftChild;
Node *leftChild = sibling->leftChild;
Node *rightChild = sibling->rightChild;
if (getColor(leftChild) == RED || getColor(rightChild) == RED) {
if (parent -> leftChild == sibling) {
if (getColor(leftChild) != RED) {
setColor(sibling, RED);
setColor(rightChild, BLACK);
rotateLeft(sibling);
sibling = sibling->parent;
leftChild = sibling->leftChild;
}
int oldColor = getColor(parent);
setColor(parent, BLACK);
setColor(leftChild, BLACK);
rotateRight(parent);
setColor(sibling, oldColor);
}
else {
//cout << "ok\n" ;
if (getColor(rightChild) != RED) {
setColor(sibling, RED);
setColor(leftChild, BLACK);
rotateRight(sibling);
sibling = sibling->parent;
rightChild = sibling->rightChild;
}
int oldColor = getColor(parent);
setColor(parent, BLACK);
setColor(rightChild, BLACK);
rotateLeft(parent);
setColor(sibling, oldColor);
}
return;
}
if (getColor(sibling) == BLACK) {
setColor(sibling, RED);
if (getColor(parent) == RED)
setColor(parent, BLACK);
else
eraseFix(parent->parent, getSibling(parent));
return;
}
if (getColor(sibling) == RED) {
Node* other = getSibling(sibling);
setColor(sibling, BLACK);
setColor(parent, RED);
if (sibling == parent->rightChild)
rotateLeft(parent);
else
rotateRight(parent);
// cout << parent->color << " " << sibling->color << "\n\n";
// (*this)._display_tree();
eraseFix(parent, otherChild(parent, other));
eraseFix(parent, sibling);
return;
}
}
4.3.4 Tổng kết:
Với thao tác delete ta sẽ chia thành các trường hợp:
- Nút cần xóa có cả hai con
- Nút cần xóa có 1 con hoặc nút cần xóa không có con nào nhưng bản thân nó là màu đỏ
- Nút cần xóa màu đen, không có con, sibling có ít nhất 1 child màu đỏ
- Nút cần xóa màu đen, không có con, sibling và 2 con của sibling đều màu đen
- Nút cần xóa màu đen, không có con, sibling màu đỏ